Eri tapoja todistaa Pythagorasin lause: esimerkkejä, kuvauksia ja arvosteluja

Yhdessä voit olla varma sataprosenttisestiprosenttia, että kysymys siitä, mikä on yhtä suuri kuin hypotenusen neliö, jokainen aikuinen ihminen rohkeasti vastaa: "Jalojen neliöiden summa". Tämä teoreema on tiukasti kiinni jokaisen koulutetun henkilön mieleen, mutta sinun on vain pyydettävä joku todistamaan sen ja sitten voi olla vaikeuksia. Muista siis miettiä eri tapoja todistaa Pythagoraanin lause.

Yleiskatsaus elämäkertaan

Pythagoraaninen lause on tuttu lähes kaikille, muttajostain syystä sen tuottavan henkilön elämäkerta ei ole niin suosittu. Se voidaan korjata. Siksi ennen kuin tutkitaan erilaisia ​​menetelmiä todistaa Pythagoraan lause, on tarpeen tutustua lyhyesti hänen persoonallisuutensa.

Pythagoras on filosofi, matemaatikko, ajattelijaAntiikin Kreikka. Nykyään on hyvin vaikea erottaa hänen elämäkertaansa tämän suuren miehen muistoista muodostuneista legendoista. Mutta seuraajiensa teoista lähtien Samoksen Pythagoras syntyi Samoksen saarella. Hänen isänsä oli tavallinen kivenleikkuri, mutta hänen äitinsä tuli jaloilta.

Legendan mukaan Pythagoras syntyiennusti naisen nimeltään Pythia, jonka kunniaksi ja nimeksi poika. Hänen ennustuksensa mukaan syntyneen pojan piti tuoda paljon hyötyä ja hyvää ihmiskunnalle. Mitä hän itse asiassa teki.

Laulun syntyminen

Nuoruutensa Pythagoras muutti SamostaEgypti tavata kuuluisia egyptiläisiä vieviä siellä. Tavattuaan heitä hän pääsi koulutukseen, ja tiesi missä kaikki suuria saavutuksia Egyptin filosofian, matematiikan ja lääketieteen.

Todennäköisesti Egyptissä Pythagoras inspiroimajesteettia ja kauneutta pyramideja ja loi suuren teorian. Tämä saattaa hyppäsi lukijoita, mutta modernit historioitsijat uskovat, ettei Pythagoras osoittanut hänen teoriaansa. Mutta hän välittää vain tietonsa seuraajilleen, jotka myöhemmin suorittivat kaikki tarvittavat matemaattiset laskelmat.

Joka tapauksessa, nykyään ei tiedetä.todistusmenetelmä tästä lauseesta, mutta useita kerralla. Nykyään on vain keksiä, kuinka tarkalleen muinaiset kreikkalaiset tekivät laskelmia, joten tässä pohdimme erilaisia ​​tapoja todistaa pythagoralaisen lause.

Pythagoraaninen lause

Ennen kuin aloitat laskennan, sinun on selvitettävä, mitä teoriaa voidaan todistaa. Pythagoralaisen lause kuulostaa näin: "Kolmiossa, jossa yksi kulmista on 90^noin, jalkojen neliöiden summa on yhtä suuri kuin hypotenuksen neliö. "

On olemassa 15 eri tapaa todistaa Pythagoraanin lause. Tämä on melko suuri määrä, joten kiinnitämme huomiota suosituimpiin.

Menetelmä yksi

Ensiksi mainitsemme, mitä meille annetaan. Nämä tiedot laajennetaan koskemaan myös muita Pythagoraanin lauseiden osoittamismenetelmiä, joten muistat välittömästi kaikki olemassa olevat nimitykset.

Oletetaan, että oikean kulmaisen kolmion annetaan, kun a ja b katetit ovat yhtä kuin c. Ensimmäinen todistusmenetelmä perustuu tarpeeseen piirtää neliö oikealta kolmelta.

Voit tehdä tämän, sinun on jalka pituus apiirtää segmentti, joka on yhtä kuin jalka ja päinvastoin. Joten neliön pitäisi olla kaksi yhtä sivua. Jäljelle jää vain kaksi rinnakkaista viivaa, ja neliö on valmis.

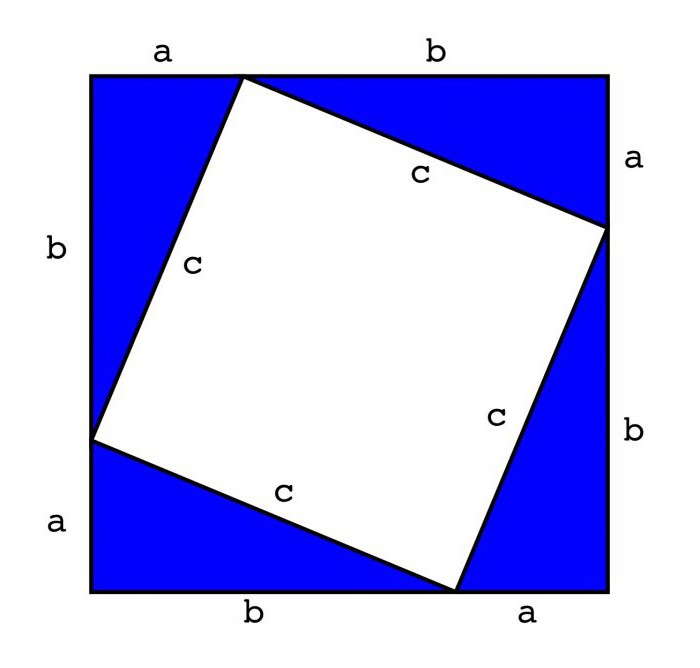
Tuloksena olevan luvun sisällä sinun täytyy tehdä enemmänyksi neliö, jonka sivu on sama kuin alkuperäisen kolmion hypotenuus. Tätä varten sinun on tehtävä kaksi rinnakkaista segmenttiä, jotka ovat yhtä kuin c ja sv. Niinpä on neliön kolme sivua, joista yksi on alkuperäisten suorakaiteen muotoisten kolmioiden hypotenuus. Jäljelle jää vain neljäs segmentti.

Tuloksena olevan kuvion perusteella voidaan päätellä, että ulomman neliön pinta-ala on (a + b)². Jos katsot kuvion sisällä, näet, että sisäisen neliön lisäksi on neljä oikeanpuoleista kolmiota. Kunkin alueen pinta-ala on 0,5.

Siksi alue on: 4 * 0.5av + s²= 2av + s²

Tästä (a + c)²= 2av + s²

Ja siksi²= a²+ sisään²

Lause on osoitettu.

Menetelmä kaksi: samanlaiset kolmiot

Tämä kaava on todiste Pythagoraan-lauseestaoli johdettu geometrian osaa koskevan lausuman perusteella samankaltaisista kolmioista. Se kertoo, että oikean kolmion jalka on keskimäärin verrannollinen sen hypotenuteen ja 90-luvun ylhäältä lähtevän hypotenuksen segmenttiin^noin.

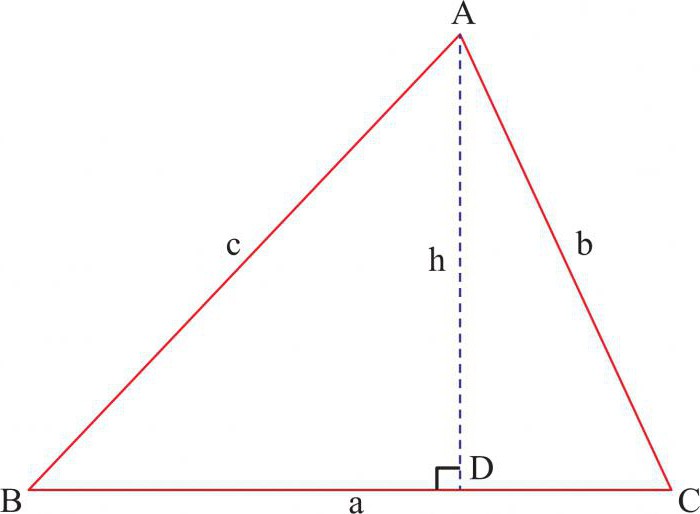
Alkuperäiset tiedot ovat edelleen samat, joten aloitamme välittömästi todistuksen. Suorita kohtisuorassa AB-segmentin SD-puolelle. Edellä olevan lausuman perusteella kolmiot jalat ovat yhtä suuret:

AC = √ AB * AD, CB = √ AB * DV.

Jotta voitaisiin vastata kysymykseen siitä, kuinka todistaa Pythagoraanin lause, todiste on määriteltävä poistamalla molemmat eriarvoisuudet.

AS²= AB * HELL ja SV²= AB * DV

Nyt meidän on lisättävä tuloksena oleva epätasa-arvo.

AS²+ SV²= AB * (HELL * LW), jossa HELL + LW = AV

Näyttää siltä, ​​että:

AS²+ SV²= AB * AB

Ja siksi:

AS²+ SV²= AB²

Pythagoraanin teoreeman todiste ja erilaiset ratkaisumenetelmät tarvitsevat monipuolista lähestymistapaa tähän ongelmaan. Tämä vaihtoehto on kuitenkin yksi yksinkertaisimmista.

Toinen laskentamenetelmä

Kuvaus eri tavoista todistaa lausePythagoras ei voi sanoa mitään mistään, ennen kuin sinä itse alkaa harjoitella itseäsi. Monet menetelmät eivät koske vain matemaattisia laskutoimituksia vaan myös uusien lukujen rakentamista alkuperäisestä kolmioista.

Tässä tapauksessa on välttämätöntä täydentää vielä yksi AF: n oikean ankkuroitu kolmio. Näin ollen nyt on kaksi kolmioa, joilla on yhteinen BC.

Tietäen, että tällaisten lukujen alueet ovat suhteessa samanlaisten lineaaristen ulottuvuuksien neliöihin, silloin:

S_ABC * kanssa²- S_AVD* sisään² = S_AVD* a²- S_IRR* a²

S_ABC* (s²-in²) = a²* (S_AVD-S_IRR)

kanssa²-in²= a²

kanssa²= a²+ sisään²

Koska eri tapoja todistaa Pythagoraan lause kahdeksasluokkalaiselle tämä vaihtoehto on tuskin sopiva, voit käyttää seuraavaa menetelmää.

Helpoin tapa todistaa Pythagoraanin lause. Arviot

Historioitsijat uskovat, että tämä oli ensimmäinen kertakäytetään todistamaan lause antiikin Kreikassa. Se on yksinkertaisin, koska se ei vaadi mitään laskelmia. Jos piirrät kuvan oikein, sen todistus siitä, että²+ sisään²= kanssa² on selvästi näkyvissä.

Tämän menetelmän ehdot poikkeavat hieman edellisestä. Todistaaksesi lause, oletetaan, että oikea kolmio ABC on isosceles.

Otamme hypotenusu AS: n neliön sivulle jaOlemme kolme sen osapuolta. Lisäksi tuloksena olevassa neliössä on tarpeen piirtää kaksi lävistävää viivaa. Joten siinä on neljä isosceles kolmioita.

AV- ja SV-ryhmiin on myös tehtävä neliö ja piirrettävä yksi ristikudosviiva kussakin niistä. Ensimmäinen suora, joka piirretään A: n yläosasta, toinen - C.

Nyt sinun on tarkasteltava tarkasti tuloksena olevaa kuvaa. Koska AC-hypotenusissa on neljä kolmiota, jotka ovat alkuperäisen ja kaksi jalkaa, tämä osoittaa tämän lauseen todenmukaisuuden.

Muuten, tämän menetelmän ansiosta Pythagoraanin lause osoittautui kuuluisaksi lauseeksi: "Pythagoralaiset housut ovat tasavertaisia ​​kaikilla suuntiin".

Todistus J. Garfieldista

James Garfield on Amerikan yhdysvaltojen 20. presidentti. Sen lisäksi, että hän jättikin historiansa merkkinä Yhdysvaltojen hallitsijana, hän oli myös lahjakas itseoppisesti.

Hänen uransa alussa hän oli tavallinenopettaja folk-koulussa, mutta pian tuli yksi korkeakoulujen johtajista. Oman itsensä kehittämiseen pyrkivä ja antanut hänelle ehdotuksen uutta teoriaa todistaakseen Pythagoraanin lauseesta. Lause ja esimerkki ratkaisusta ovat seuraavat.

Ensin sinun on kiinnitettävä kaksi paperiaoikealle kulmikkaat kolmiot niin, että jompikumpi niistä on jatkoa toiselle. Näiden kolmiotien pisteet on yhdistettävä, jotta ne päätyisivät puolisuunnikkaan.

Kuten tiedetään, puolisuunnikkaan pinta-ala on yhtä suuri kuin sen pohjan puolikiven summa ja sen korkeus.

S = a + b / 2 * (a + b)

Jos tarkastelemme tuloksena olevaa trapetsia kuviona, joka koostuu kolmesta kolmiosta, sen alue löytyy seuraavasti:

S = AV / 2 * 2 + s²/ 2

Nyt sinun täytyy tasapainottaa kaksi lähdekoodia

2av / 2 + s / 2 = (a + b)²/ 2

kanssa²= a²+ sisään²

Pythagoraani-lauseesta ja sen todistamisesta voit kirjoittaa useampaa kuin yhtä oppikirjan osaa. Mutta onko järkevää, kun tätä tietoa ei voida toteuttaa käytännössä?

Pythagoraanin teoreeman käytännön soveltaminen

Valitettavasti nykyaikaisissa kouluohjelmissaTätä teoriaa voidaan käyttää vain geometrisissa ongelmissa. Valmistujat lähtevät pian koulun seinistä, eivätkä koskaan tiedä, miten heidän tietämystään ja taitojaan sovelletaan käytännössä.

Käytä itse asiassa Pythagoraanin lausejokainen voi hoitaa jokapäiväistä elämää. Ei pelkästään ammattitoiminnassa vaan myös tavallisissa kotitöissä. Tarkastellaan useita tapauksia, joissa Pythagoraanin lause ja menetelmät sen todistamiseksi voivat olla äärimmäisen välttämättömiä.

Viestinnän lause ja tähtitiede

Näyttäisi siltä, ​​että tähdet ja kolmiot voidaan liittää paperiin. Itse asiassa tähtitiede on tieteellinen ala, jossa pythagoralaista lause on laajalti käytetty.

Tarkastellaan esimerkiksi valonsäteen tilaa avaruudessa. Tiedetään, että valo liikkuu molempiin suuntiin samalla nopeudella. Valokeilan liikuttavaa AB-liikerataa kutsutaan l. Ja puolet ajasta, jonka valon täytyy saada pisteestä A pisteeseen B, soitamme T. Ja palkin nopeus - C. Näyttää siltä, ​​että: c * t = l

Jos katsot tämän toisen säteenesimerkiksi avaruuslinjasta, joka liikkuu nopeudella v, niin kun tällainen kehon havainnointi tapahtuu, nopeus muuttuu. Tällöin jopa stationaariset elementit liikkuvat nopeudella v vastakkaiseen suuntaan.

Oletetaan, että koominen vuoraus kelluu oikealle. Sitten pisteet A ja B, joiden välissä säde heitetään, siirtyvät vasemmalle. Lisäksi kun palkki liikkuu pisteestä A pisteeseen B, A-pisteellä on aikaa liikkua ja näin ollen valo saapuu uuteen kohtaan C. ").

d = t "* v

Ja jotta löydettäisiin etäisyys, jonka valonsäde voisi kulkea tänä aikana, sinun täytyy nimetä puolet uuden pyökin polusta ja saada seuraava ilmaus:

s = c * t "

Jos kuvitat, että valopisteet ovat C ja B, jaKoska avaruusalusta on isosceles-kolmion kärki, segmentti pisteestä A linjalle jakaa sen kahteen oikeaan kolmioon. Siksi Pythagoraanin lauseen ansiosta löydät etäisyyden, jonka valonsäde voisi kulkea.

s² = l² + d²

Tämä esimerkki ei tietenkään ole menestyksekkäintä, sillä vain harvat voivat olla kyllin kyllin kokea sitä käytännössä. Siksi pohdimme tämän lauseen soveltamisen arkipäiväisempää versiota.

Matkaviestinsignaali

Nykyaikaa ei voi enää kuvitella ilman älypuhelinten olemassaoloa. Mutta kuinka paljon heistä heistä olisi proc, jos he eivät voineet yhdistää tilaajia matkaviestinnän kautta?

Matkaviestinnän laatu riippuu suoraanmatkaviestinoperaattorin antennin korkeus. Jotta voit laskea, kuinka pitkälle puhelin voi vastaanottaa signaalin mobiilitornista, voit soveltaa Pythagoraan lause.

Oletetaan, että sinun on löydettävä kiinteän tornin likimääräinen korkeus, jotta se voi levittää signaalia 200 kilometrin säteellä.

AB (tornin korkeus) = x;

SU (signaalin lähetyksen säde) = 200 km;

OS (maapallon säde) = 6380 km;

Täältä

OB = OA + ABOV = r + x

Pythagoraanin lauseen soveltaminen huomaa, että tornin minimikorkeuden tulisi olla 2,3 kilometriä.

Pythagoralainen lause jokapäiväisessä elämässä

Kumma kyllä, Pythagoraanin lause voi osoittautuahyödyllisiä myös kotimaisissa asioissa, kuten esim. kaapin korkeuden määrittäminen. Ensisilmäyksellä ei ole tarvetta käyttää tällaisia ​​monimutkaisia ​​laskutoimituksia, koska mittaustulokset voidaan mitata vain mittakaavalla. Mutta monet ihmettelevät, miksi kokoonpanoprosessissa on tiettyjä ongelmia, jos kaikki mittaukset on tehty enemmän kuin tarkasti.

Tosiasia on, että vaatekaappi on menossavaakasuorassa asennossa ja vain silloin nousee ja asennetaan seinää vasten. Siksi rakenteen nostamisen prosessissa kaapin sivuseinän on mentävä vapaasti läpi huoneen korkeus ja lävistäjä.

Oletetaan, että vaatekaappi on syvyys 800 mm. Etäisyys lattiasta kattoon - 2600 mm. Kokenut huonekaluvalmistaja sanoo, että kaapin korkeus olisi 126 mm pienempi kuin huoneen korkeus. Mutta miksi juuri 126 mm? Harkitse esimerkkiä.

Ihanteellisten kaapin mitojen avulla tarkistamme Pythagoraanin lauseen vaikutuksen:

AC = √ AB²+ √ВС²

AC = 74 2474²+800²= 2600 mm - kaikki sopii.

Oletetaan, että kaapin korkeus ei ole 2474 mm, mutta 2505 mm. sitten:

AC = 502505²+ √800²= 2629 mm.

Siksi tämä kaappi ei sovi tähän huoneeseen. Koska nostettaessa sitä pystysuorassa asennossa, sen runko voi vaurioitua.

Ottaen huomioon eri tapoja todistaaPythagorean teoreetat eri tutkijoiden mukaan, voimme päätellä, että se on enemmän kuin totta. Nyt voit käyttää päivittäisessä elämässä saatuja tietoja ja olla täysin varma, että kaikki laskelmat eivät ole vain hyödyllisiä, vaan myös totta.